深度学习|“植树问题”引发的头脑风暴
让学生站立在课堂中央,成为学习的主体。教师就像一位提灯的引路人,用精心打磨的教学环节,用一次又一次精准的提问追问,激发出学生的探究热情,点燃孩子们的思维火花,让思考深入再深入,让深度学习自然生成。
近日,王府外国语小学部数学组教师房继英就人教版《小学数学》(第九册)中的“植树问题”一课,带领五(6)班同学开启了一场酣畅淋漓的数学深度学习之旅。
激发探究热情
让学生体会身边处处是数学的同时,直观清晰地领会“间隔”的含义,在不知不觉中展开对数学问题的探索,激发与间隔有关的植树问题的探究欲望。
让课堂减负增效
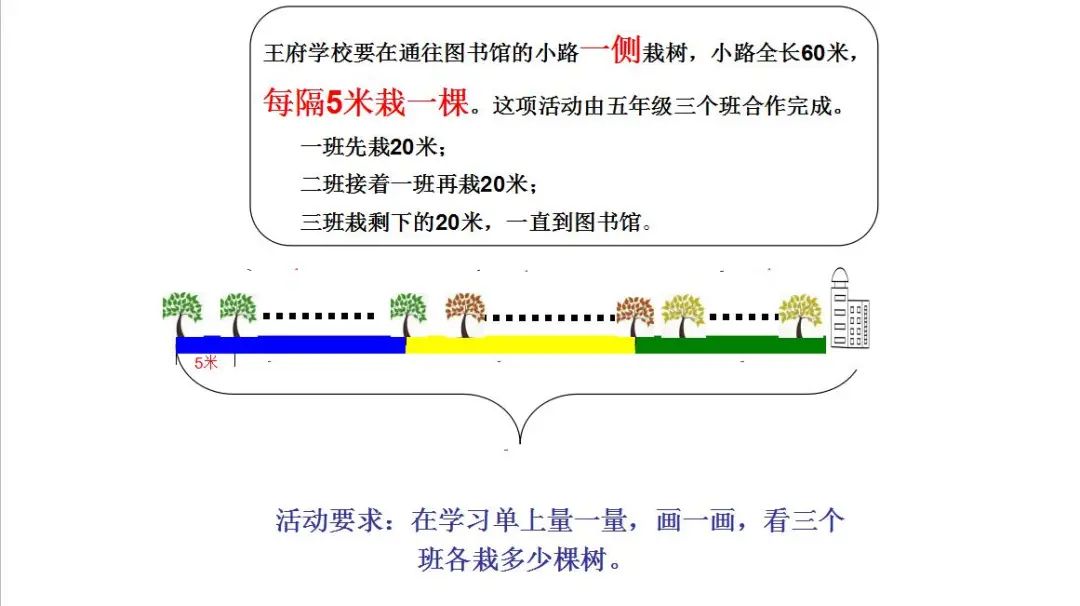
感受数学之美

突然产生的认知冲突,教室里一下安静了下来,忽然一只小手高高举起:“1000÷5=200, 200+1=201。”话音刚落,掌声响起。对于学生的积极思考、成功解题,我及时给予了肯定:“在计算复杂问题的时候,可以用计算来解决。”随后自然返回到刚刚经历的20米小路上植树的情况,研究用计算解决这类问题的好方法。
让学生体会到研究问题可以从简单入手,将困难的变为容易的,将复杂的变为简单的,用这样的方法,可以有效地解决问题。把抽象的数学化归思想渗透在教学中,让学生在“润物细无声”中体验到数学思想方法的价值,提高思维的素质。
体会思想方法
我不动声色地问:“有问题吗?”
很多只小手举起来:“20÷5=4后面的单位不能是“棵”,应该是4个间隔。”
“为什么?你到前来面指一指。”
学生在小树模型处指出间隔,我又重新强化了刚刚这位同学的意思:一边画标志一边说:一个间隔1棵树,一个间隔1棵树……一共几个间隔?几棵树?
学生:四个间隔4棵树。至此,成功明确了4后面的单位是4个间隔的“个”。
让学生在经历数学建模的过程中,体验一一对应、数形结合的数学思想方法。
我再次发问:还有问题吗?
片刻,一生举手:4+1=5(棵)中的“1”是什么呢?为什么+1?
师:“你的问题真有价值(大拇指送给他)!是啊,“1”是什么呢,谁到前面来找一找、指一指“1”在哪里?”很多同学踊跃举手,一生到前面来指向了小树模型中最前面的1棵,同时说,也可以是最后1棵,热烈的掌声再次齐刷刷地响起!
我又一次发问:还有问题吗?
生:没有了。
师:真的没有问题了吗?
一个同学慢慢举起手犹豫着问道:那4个间隔为什么跟1棵树加在一起呢?
这时,学生中有人悄声回应,然后有人勇敢举起手:那是刚刚说的4个间隔对应的4棵树。掌声哗然!
师:“那谁能到前面来解释一下20÷5=4(个),4+1=5(棵)这两个算式?”随着同学的解释,师随即板书:全长、间距、间隔数、棵数,并带着同学一起表达:“20除以5等于4个间隔,4个间隔对应着4棵树,再加上前面的1棵,就等于5棵树。” 有序思维的整理,让学生在头脑中建立起植树问题模型的初步形态。

回归数学本真
学生在列式与表述中进一步体会和巩固着头脑中数学模型的初步形态,同时又有极限思想的渗透。小结:“只要我们掌握了方法,无论多复杂的问题我们都能解决。”强调和总结了数学思想方法的重要性。
接着观察刚刚生成的算式:“哪里变了、哪里没变?”同学们在变与不变中总结出两端都栽的情况:棵数=间隔数+1。
我接着启发学生猜想:“两端都栽的情况是棵数=间隔数+1,那只栽一端和两端不栽的情况,棵数和间隔数之间会不会也存在某种关系呢?”引发猜想,推进探究进程。
然后,孩子们信心满满地乘胜讨论、猜想、推理、验证,迁移刚刚得到的结论,将植树问题的三种情况成功建立关系,很快得出只栽一端的情况:棵数=间隔数;两端不栽的情况:棵数=间隔数-1 。
“自此我们又得出三个式子,请同学再仔细观察,三个式子哪里变了、哪里没变?”同学们通过对比,发现三个式子中变的是:有的是棵数等于间隔数加1,有的是棵数等于间隔数,有的是棵数等于间隔数减1;不变的是三种情况棵数都与间隔数有关。
此时我赶紧追问:“棵数都与间隔数有关,那间隔数重不重要?间隔数这么重要那怎么计算呢?”通过刚刚深度探究的经历和清晰有序的板书,孩子们很快得出“全长÷间距=间隔数”。环环相扣的教学环节,一切都在徐徐推进中水到渠成般自然生成。
教师及时的追问,提高了学生思维活动的完整性、准确性。同时,老师迅速捕捉课堂随机生成的问题,又引发学生针对问题进行深入思考。
沟通本质
基于此,我为全课小结这样问道:“植树问题难道仅仅是植树吗?”一个问题抛出来,思维急速运转的孩子们仿佛被泼了一瓢冷水,但很快就反应过来:“不是!”
答案虽然是对的,但是我知道,其实孩子们只是从感觉上得出的答案,并不知道到底还有哪些问题属于植树问题。趁着孩子们挫败感还未滋生,我“体谅”地接着说“那还是什么呢?让我们来一起看一看!”
课件展示出的方队、带扣子的衬衫、公交车路线、锯木头等等,每出示一种情况我都会追问:“这是植树问题吗?树在哪里?是哪种情况?”
孩子们的眼界被打开了,教室里顿时又沸腾起来!范例的启发,让孩子又想到了类似的多种情况并能迁移理解到什么是树什么是间隔。趁着孩子们处于思维的高潮期,我结合课件不失时机地问道:“这些“树”都长在了哪里呀(抽象出线和点)?这些树实质是不是线上的“点”啊?”教室里又一片恍然大悟的掌声。
今天课堂中教师的有效提问,学生有价值的质疑,有效保证了课堂交流的持续深入与良好的情绪体验。鼓励和引发学生欣赏文本信息、欣赏同伴发言的勇气、欣赏他人的不同见解、欣赏同学乐于分享的胸襟、欣赏自己的独特个性,自信表达、愿意倾听、积极思考、乐于交流,让每一个个体在深度交流中实现知识获得、情感发展和能力形成,是过去、现在和将来我们一直秉承的教育理念和努力的方向。
编辑|子婷
摄影|子婷
审核|Amanda


